

胆拖优化组合到现在共出现了两种胆拖式投注。一种是全胆拖投注,另一种是复式胆拖投注。
大家都知道一场足球比赛只有三个结果,即胜、平、负,因此在投足彩时,只要每场比赛都投三选的复式就肯定能中一等奖,但这显然是不现实的,这样投入的资金太大,结果肯定是得不偿失。有没有一种方法可以在相对低投入的基础上保中头奖?答案是肯定的。我们的胆拖优化组合投注很好地解决了这个问题。全胆拖投注的投注方式是这样的:首先由彩民对14场比赛投一个单注,这个单注自然应是彩民认为最有可能出现的结果,它将作为后面胆拖优化组合合成复式时的“胆包”,由彩民自主选择这14场比赛至少可以猜中的场次数,这个场次数就是“胆包”中“胆”的个数,然后进行“胆包”之外的“拖”的投注便可以了。全胆拖投注就是除了“胆”之外的结果都作为“拖”,也就是说,14场比赛中的每一场比赛彩民都选择三个结果,不同的投注的区别就是“胆”的选择的不同和“拖”的选择顺序的不同,例如在某一轮竞猜中有国际米兰对阵尤文图斯,某彩民把主队获胜作为“胆包”中的一个“胆”,而把主队和客队打平作为次选,主队落败作为末选,所有的次选和末选构成了“拖”。只要保证了“胆包”中“胆”的个数,经过胆拖优化组合处理的投注中必然会有一个一等奖和若干个二等奖,二等奖的个数取决于首选猜中的场次数和次选与末选的顺序。软件在处理数据时是按照这样的原理进行组合的:首先从彩民的首选14场比赛的结果即我们所说的“胆包”中随机抽取N个结果,(N=彩民所选择的首选所能保证猜对的场次数,也就是彩民所确定的“胆”的个数,0≤N≤14),然后用这N个投注结果跟彩民所选的剩下的(14-N)个投注进行排列组合。这便完成了一轮的组合,接着再从首选中选择N+1个结果,按照上面的原则进行第二轮排列,如此类推下去,直到N=14时为止。这样,就完成了整个投注过程。
以上是全胆拖投注的数学原理,这种投注方式可以很好地保中一等奖,但随着彩民投注水平的提高和不断地采用这种投奖方式投注,一等奖产生的个数也随之上升,这就造成了一等奖奖金的减少。后来又在原有的全胆拖投注基础上发明了复式胆拖投注。复式胆拖投注的投注过程是这样的:先由彩民对14场比赛投一个单注,这个单注自然应是彩民认为最有可能出现的结果,这个单注将作为后面胆拖优化组合合成复式时的“胆包”,接着由彩民自主选择这14场比赛至少可以猜中的场次数(N),这个场次数就是“胆包”中“胆”的个数。接着对这14场比赛在原有的一注的基础上进行复式投注,使这个大复式里有一个一等奖存在,然后就可以点击“投注”了。这时的组合投注原理是:首先从彩民的首选14场比赛的结果中随机抽取N个结果,然后与剩下的(14—N)个结果的次选和末选进行排列组合。彩民不必担心大复式投注使投注资金膨大,因为把所有的场次都投复式所投入的资金,也仅仅跟全胆拖投注相同首选场次的投入资金相同。
胆拖优化组合技术是一次投注理念的重大转变和突破,复式投注存在一个致命的天然缺陷,就是忽略了投注选择的概率差异,如一场比赛主队实力远远高于客队,而考虑到冷门的因素,你选择了310,但是其中出现3的概率将肯定大于出现1和出现0的概率,因14场目前只开出9期,数据尚不呈规律性,故仍以13场足彩时的数据为统计依据,如足彩第02022期(13场)为例分析,我们来分析一下3、1、0的概率情况,下面是我们在本书的前面已经介绍给大家的综合国内多家媒体所选择的一个复式投注,具体投注情况如下表:
|
场次 |
对阵双方 |
投注结果 |
正确结果 |
|
1 |
亚特兰大—AC米兰 |
0 |
0 |
|
2 |
博洛尼亚—布雷西亚 |
310 |
3 |
|
3 |
科莫—皮亚琴察 |
10 |
1 |
|
4 |
国际米兰—尤文图斯 |
310 |
1 |
|
5 |
拉齐奥—佩鲁贾 |
3 |
3 |
|
6 |
摩德纳—帕尔马 |
30 |
3 |
|
7 |
都灵—切沃 |
310 |
3 |
|
8 |
科特布斯—柏林赫塔 |
0 |
0 |
|
9 |
纽伦堡—斯图加特 |
310 |
0 |
|
10 |
慕尼黑1860—沙尔克04 |
310 |
3 |
|
11 |
勒沃库森—凯泽斯劳滕 |
31 |
3 |
|
12 |
朗斯—阿雅克肖 |
31 |
1 |
|
13 |
色当—雷恩 |
30 |
0 |
在上面的13场比赛中,10场买了主队胜即有10个3,有8场买了平即有8个1,另外还有10个0,它们之间的比例基本上是相同的,但凡是有点基本足彩常识的人都知道主队获胜的几率要明显大于打平或是客队获胜,我们通过对过去的足彩竞猜的数据统计也得到了相同的结论,下面是我们通过计算得到的大致的3、1、0之间的比例关系。
首先让我们对过去的一些足彩中奖数据进行分析。
我们统计了足彩01001期~02027期的中奖号码,其原始资料为如下:
|
期数 |
胜场数 |
平场数 |
负场数 |
胜平负比例 |
|
01001 |
5 |
4 |
4 |
5∶4∶4 |
|
01002 |
7 |
3 |
3 |
7∶3∶3 |
|
01003 |
5 |
7 |
1 |
5∶7∶1 |
|
01004 |
6 |
3 |
4 |
6∶3∶4 |
|
01005 |
7 |
1 |
5 |
7∶1∶5 |
|
01006 |
8 |
1 |
4 |
8∶1∶4 |
|
01007 |
8 |
3 |
2 |
8∶3∶2 |
|
01008 |
5 |
1 |
7 |
5∶1∶7 |
|
01009 |
6 |
3 |
4 |
6∶3∶4 |
|
02001 |
5 |
6 |
2 |
5∶6∶2 |
|
02002 |
6 |
6 |
1 |
6∶6∶1 |
|
02003 |
7 |
1 |
5 |
7∶1∶5 |
|
02004 |
3 |
7 |
3 |
3∶7∶3 |
|
02005 |
6 |
6 |
1 |
6∶6∶1 |
|
02006 |
5 |
2 |
6 |
5∶2∶6 |
|
02007 |
4 |
3 |
6 |
4∶3∶6 |
|
02008 |
5 |
5 |
3 |
5∶5∶3 |
|
02009 |
8 |
1 |
4 |
8∶1∶4 |
|
02010 |
7 |
4 |
2 |
7∶4∶2 |
|
02011 |
7 |
4 |
2 |
7∶4∶2 |
|
02012 |
4 |
3 |
6 |
4∶3∶6 |
|
02013 |
5 |
3 |
5 |
5∶3∶5 |
|
02014 |
7 |
2 |
4 |
7∶2∶4 |
|
02018 |
4 |
3 |
6 |
4∶3∶6 |
|
02019 |
5 |
3 |
5 |
5∶3∶5 |
|
02020 |
5 |
5 |
3 |
5∶5∶3 |
|
02021 |
8 |
3 |
2 |
8∶3∶2 |
|
02022 |
6 |
3 |
4 |
6∶3∶4 |
|
02023 |
7 |
5 |
1 |
7∶5∶1 |
|
02024 |
4 |
4 |
5 |
4∶4∶5 |
|
02025 |
7 |
3 |
3 |
7∶3∶3 |
|
02026 |
7 |
3 |
3 |
7∶3∶3 |
|
02027 |
7 |
5 |
1 |
7∶5∶1 |
为更直观地了解胜平负的情况,我们将结果反映到下图中:
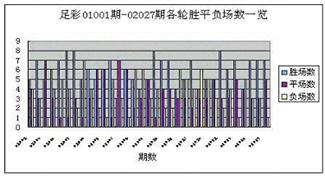
这样一来,我们便可以清楚地看到,每轮足彩的胜平负场次的差别,最多的时候是7场,最少的时候只有1场,而像7场这样的差距,还是在极个别的时候才出现,大多数情况下,胜平负场次的差距基本维持在±2场或3场左右。这样的差距,和大复式里某些注中表现出来的8、9场甚至是十几场的差距,乃至出现一个结果包满13场的情况,是大相径庭的。
我们还对历史足彩的每轮胜平负场次作了平均汇总分析,得出的结果如下图所示:
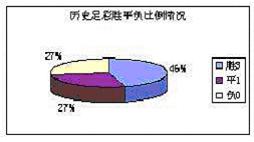
可以看出,足彩每轮的胜平负场次比例基本保持在“6∶3.5∶3.5” 左右,其中胜场最多,平场和负场平分秋色,但从细里看,负场(每轮平均为3.545)要比平场(每轮平均为3.515)多出0.03,从而负场每轮出现的概率要比平场高。胜平负场次出现的概率由大到小分别为“胜场—负场—平场”,而且胜场对负场和平场的差距也大概在19%左右。
可见,有的场次虽然我们选择了两个或者是三个结果,但它们出现的几率是不同的,而我们在用复式投注时,却为“小概率事件”和“大概率事件”付出了同样比例的资金,这很显然是一种资金的浪费。胆拖优化组合技术可以将你的复式投注选择首选、次选、末选,你可以把你认为中奖概率最大的结果放到首选列,其次是次选、末选。胆拖优化组合将首选的结果组成的一个单注作为了“胆包”,也就是确定了一个中心。次选和末选(当然也可以不选)作为“拖”,“拖”围绕着“胆包”中的“胆”旋转,这就大大提高了首选在投注中的使用率。另外次选和末选的概率也不相同,末选的概率最低,在首选相同的情况下,相同的结果如果处于不同的次选和末选位置将直接影响二等奖的个数。经过这样的优化组合投注与原复式相比,投注资金将节省2~10倍甚至更多,节约的比例取决与你首选猜中的场次及彩民所选择的复式的大小。